■記事リスト / ▼下のスレッド
/ ▲上のスレッド
| ■50281 / 親記事) |
複数の点によって構成される多角形を相互の距離情報から類推する方法
|
□投稿者/ めにぃ 一般人(1回)-(2020/04/13(Mon) 18:18:39)
 | お世話になります。以下の点をご教授いただければ幸いです。
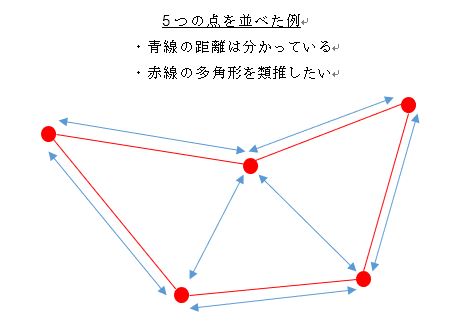
今、4つ以上の複数の点があるとします。これらの点を囲碁のように、何かを囲うような形に、適当な間隔で並べてゆきます。1つの多角形(面)を構成するように並べ、ねじれた形に並べる事はしません。この時、すべての点のすべての組み合わせについて、点間の距離は分かっていますが、角度は分かりせん。
このような条件で、各点を線分で結んだ図形(多角形)を類推する方法はあるでしょうか。無理な場合、どのような条件を付加すれば、類推可能になるでしょうか。
よろしくお願いいたします。
|
|
455×326 => 250×179
1586769519.jpg/24KB
|
|
▽[全レス6件(ResNo.2-6 表示)]
| ■50283 / ResNo.2) |
Re[2]: 複数の点によって構成される多角形を相互の距離情報から類推する方法
|
□投稿者/ めにぃ 一般人(2回)-(2020/04/13(Mon) 20:21:02)
 | どれか1つの点を原点(0,0)とした時、他のすべての点の座標を知りたいと思います。
添付図では説明上、各点をあるべき座標にプロットしていますが、実際には各々の点については他の点との直線距離が分かっているだけで、最初からこのような図形になっていると認識できているわけではありません。
よろしくお願いします。
|
|
|
| ■50284 / ResNo.3) |
Re[3]: 複数の点によって構成される多角形を相互の距離情報から類推する方法
|
□投稿者/ らすかる 一般人(13回)-(2020/04/13(Mon) 22:22:57)
 | 裏返しだけはわかりませんが、それを除けば特定できると思います。
|
|
|
| ■50285 / ResNo.4) |
Re[4]: 複数の点によって構成される多角形を相互の距離情報から類推する方法
|
□投稿者/ めにぃ 一般人(3回)-(2020/04/13(Mon) 22:35:38)
 | 可能ですか!
計算方法を教えていただければ幸いです。
|
|
|
| ■50286 / ResNo.5) |
Re[5]: 複数の点によって構成される多角形を相互の距離情報から類推する方法
|
□投稿者/ らすかる 一般人(14回)-(2020/04/14(Tue) 00:06:11)
 | 点を順にA,B,C,…とします。
Aは原点にします。
Bはx軸上の正の(AB,0)にとります。
Cが直線AB上にないとき、Cをy>0の範囲にとることにすれば
ただ一つに決まります。
このCの位置の計算方法はいろいろありますが、
三角関数を使ってよければ
cos∠CAB=(AB^2+AC^2-BC^2)/(2AB・AC)
によりcos∠CABを求め、sin∠CAB=√{1-(cos∠CAB)^2}により
sin∠CABを求めてから
(x,y)=(AC/AB)(B-A)
C=A+(xcos∠CAB-ysin∠CAB,xsin∠CAB+ycos∠CAB)
のように計算するのが簡単かと思います。
次のDの位置はほぼ同様ですが、
例えば△BCDを考えるときに直線CDのどちら側にあるかを
判定する必要があります。
まず上と同様に
cos∠DBC=(BC^2+BD^2-CD^2)/(2BC・BD)
sin∠DBC=√{1-(cos∠DBC)^2}
(x,y)=(BD/BC)(C-B)
D=B+(xcos∠DBC-ysin∠DBC,xsin∠DBC+ycos∠DBC)
または
D=B+(xcos∠DBC+ysin∠DBC,xsin∠DBC-ycos∠DBC)
のように二つの候補を求めますが、
どちらが適解かはADの距離で判定します。
どちらで計算してもADと一致する場合は、どちらをとっても構いません。
残りの点も同様ですが、
最後の適解判定で既に決まっている点を判定できるまで順に使います。
つまり上と同様にして△GHIからIの候補を二つ求まったとき、
AIで判定できればそちら、判定できない場合はBIで判定、
それでも判定できなければCIで判定、…、最後にFIで判定しても
決まらないときはどちらでもOKです。
(判定できないのはA〜Hが一直線に並んでいる場合だけです。)
これを繰り返せばすべての点の位置が決まりますね。
# 「AB」は線分ABの長さ、「BD」は線分BDの長さ、他も同様です。
# B-Aのように単独で使った場合はその位置(ベクトル)です。
# もし三角関数がわからない場合でも、cos∠CABをc、sin∠CABをs
# のように単純な変数と考えて計算すればOKです。
# cos∠CABが1または-1の場合はA,B,Cが一直線に並んでいますので
# 計算を分ける必要があるかも知れません。
# cos∠CABが1より大きいか-1より小さい場合は、点間の距離が正しくなく
# AB,BC,CAが三角形の成立条件を満たしていません。
# また、cos∠CABが1または-1に非常に近い値の場合、計算誤差により
# 正しく求まらない可能性があります。
# 複数の点が同じ位置だといろいろ不都合が起こりますので
# それはないようにして下さい。
|
|
|
| ■50287 / ResNo.6) |
Re[6]: 複数の点によって構成される多角形を相互の距離情報から類推する方法
|
□投稿者/ めにぃ 一般人(4回)-(2020/04/14(Tue) 07:01:02)
 | 具体的で実戦的な答えをありがとうございました!
またよろしくお願いいたします!
|
|
|
■記事リスト /
レス記事表示 →
[親記事-6]
|
