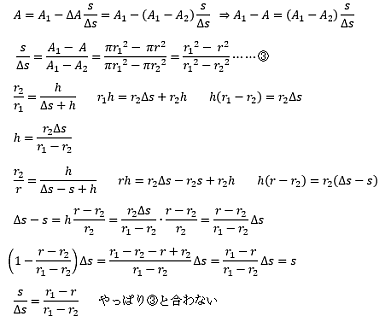���L�����X�g / �����̃X���b�h
/ ����̃X���b�h
| ��52393 / �e�L��) |
�@�K�E�X�����̕����a
|
�����e��/ ����҂�5�� ��ʐl(3��)-(2023/12/01(Fri) 15:46:40)
 | ������ł��B
���O�����W���̎l�����藝�Ƃ����̂�����
�C�ӂ̎��R����4�ȉ��̎��R���̕������̘a�ŕ\���܂��B
������K�E�X�����Ɋg���ł��Ȃ������l���܂����B
�������A������a,b�ɑ���x=a+bi�Ƃ����x^2=(a^2-b^2)+(2ab)i�ƂȂ���
�K�E�X����x��Im(x^2)�͏�ɋ����ɂȂ��Ă��܂��܂��B
�܂�A�K�E�X����y��Im(y)����Ȃ��
�K�E�X�����̕������̘a�ɂ͕\���Ȃ��Ƃ������ƂɂȂ�܂��B
�K�E�X����y��Im(y)�������Ȃ��
�K�E�X�����̕������̗L���̘a�ɂ͕\����ƌ�����ł��傤��?
�ؖ��܂��͔���̕�����������܂����狳���Ă��������B
��낵�����肢�������܂��B
|
|
|
��[�S���X8��(ResNo.4-8 �\��)]
| ��52398 / ResNo.4) |
�@Re[1]: �K�E�X�����̕����a
|
�����e��/ ����҂�5�� ��ʐl(5��)-(2023/12/02(Sat) 16:25:27)
 | ���ȃ��X�ł��B
�P����(n+1)^2-n^2=2n+1���g���ƁA������a�ɑ��Ď�����n�����݂���
a����Ȃ��a=(n+1)^2+(ni)^2�ƕ\���܂����A
a�������Ȃ��a=(n+1)^2+(ni)^2+1^2�ƕ\���܂��B
�܂�A������a��3�ȉ��̃K�E�X�����̕������̘a�ɕ\���邱�ƂɂȂ�܂��B
�܂��A(1+i)^2=2i�Ȃ̂ŁA������b�ɑ��ăK�E�X����p,q,r�����݂���
b*2i=(p^2+q^2+r^2)(1+i)^2��2bi��3�ȉ��̃K�E�X�����̕������̘a�ɕ\���邱�Ƃ�������܂��B
�Z�߂�Aa+2bi�Ƃ����K�E�X������6�ȉ��K�E�X�����̕������̘a�ɕ\����ƌ�����Ǝv���܂��B
�ܘ_�A���X6�Ƃ������Ƃ������������ŏ�肭�I�ׂ����Ə��Ȃ����ɂł���̂�������܂���B
�����Ə��Ȃ����ő����Ƃ����ؖ�������܂����狳���Ă��������B
��낵�����肢�������܂��B
|
|
|
| ��52399 / ResNo.5) |
�@Re[1]: �K�E�X�����̕����a
|
�����e��/ WIZ ��ʐl(8��)-(2023/12/02(Sat) 23:59:39)
 | a, b��L�������Ƃ���A
(a+2bi)-(1+bi)^2 = a-1+b^2
�܂��Aa-1+b^2�͗L�������Ȃ̂ŁA��Ȃ玿��҂���̎��������@�̒ʂ�A
a-1+b^2 = (2�ȉ��̃K�E�X�����̕����̘a)
�ƕ\����B
���ɁA(x^2+y^2)(p^2+q^2) = (xp+yq)^2+(xq-yp)^2�Ƃ����W����p����ƁA
# 2�ȉ��̕������̘a�ƂȂ鐔���u�̐ς�2�ȉ��̕������̘a�ƂȂ�Ƃ������ƁB
2 = 1^2+1^2�ł��邱�Ƃ���A2�̎��R�����2�ȉ��̎��R���̕����̘a�ƌ�����B
a-1+b^2�������Ȃ�A
a-1+b^2 = (2�̎��R����)*(�)
= (2�ȉ��̎��R���̕����̘a)*(2�ȉ��̃K�E�X�����̕����̘a)
= (2�ȉ��̃K�E�X�����̕����̘a)
�ƕ\����B
����āA
a+2bi = (1+bi)^2+(2�ȉ��̃K�E�X�����̕����̘a)
��3�ȉ��̘a�ƂȂ�܂��ˁB
|
|
|
| ��52400 / ResNo.6) |
�@Re[1]: �K�E�X�����̕����a
|
�����e��/ ����҂�5�� ��ʐl(6��)-(2023/12/04(Mon) 09:20:23)
 | WIZ�l�ԐM���肪�Ƃ��������܂��B���炪�x��Đ\����܂���B
3�ȉ��̘a�ƂȂ�̂ł��ˁB�����ł��B
������Ē�����2�̕������̘a����@�ɕ��Ă���Ƃ����藝��
�t�F���}�[�̓��藝�ł��g�p����Ă���W���ł��ˁB
�K�E�X�������܂߂ĕ������ł���Η��p�ł���Ƃ������ƂɋC���t���܂���ł����B
���Ȃ鋻���͂ǂ����Ă�3�K�v�ƂȂ�Im(y)�������ł���K�E�X����y�͑��݂���̂�?
���݂���Ȃ�L����������? �ǂ̂悤�ȏ����̃K�E�X������?
�Ȃǂł��ˁB
�K�E�X�������f���������ł��܂�����
�K�E�X�����̑f���̃K�E�X�����̕������̘a�ɕ\������͂��邱�ƂɂȂ�Ǝv���܂��B
�Ƃ͌����Ă��A2=(-i)(1+i)^2�ł���Im(-i)��Im(1+i)����ł�����
�P��-i��f��1+1�ł��K�E�X�����̕������̘a�ɕ\����Ȃ����̂����݂����͍͂��������܂���B
�K�E�X����x��y��Im(x)��Im(y)����ł����Ă�Im(xy)�͋����ƂȂ邱�Ƃ�����̂�
�����̃C�f�A���_�̂悤�Ȃ��̂ɂȂ�̂�������܂���B�z���ł����B
��낵�����肢�������܂��B
|
|
|
| ��52401 / ResNo.7) |
�@Re[1]: �K�E�X�����̕����a
|
�����e��/ WIZ ��ʐl(9��)-(2023/12/05(Tue) 10:08:19)
 | 2023/12/05(Tue) 14:34:26 �ҏW(���e��)
�u�K�E�X�����̑f���v���u�K�E�X�f���v�A
�u�K�E�X�����̕������v���u�K�E�X�������v�ƋL�ڂ��邱�Ƃɂ��܂��B
�K�E�X�����̐ςɂ��čl����ꍇ�A��ɓ������ɒ��ӂ���K�v������܂��B
�m�������L���f���ł���K�E�X�����̓K�E�X�f���ƂȂ�A�ȉ��̕��ނƂȂ�܂��B
(1)�L���f��2�̖̃K�E�X������1+i�̓K�E�X�f���ł���B
2 = (-i)((1+i)^2)�ł����A1+i�̓������ɂ�-1-i, 1-i, -1+i������܂��B
������������P��i�̌W������Ȃ̂ŁA�K�E�X�������̘a�ɂ͕\���܂���B
(2)�L���f��p��p �� 1 (mod 4)�̏ꍇ��p�̖ł���P���łȂ��K�E�X�����̓K�E�X�f���ł���B
�t�F���}�[�̓��藝�ɂ��A����L������a, b�����݂���p = a^2+b^2�ƕ\���܂��B
����āAp = (a+bi)(a-bi)�ƕ\����Aa+bi��a-bi�͋����ȃK�E�X�f���ƂȂ�܂��B
a, b�̈���͋����ő����͊�Ȃ̂ŁA�ŏ�����a�͊��b�͋����Ƃ��Ă���ʐ��������܂���B
����ƁA����L������u, v�����݂���a = 2u-1, b = 2v�ƕ\���܂��B
���R�������P�����ł����A(2u-1)+2vi = (u+vi)^2+(v-(u-1)i)^2���A
(2u-1)-2vi = (u-vi)^2+(v+(u-1)i)^2�Ȃ̂ŁA
a+bi��a-bi��2�̃K�E�X�������̘a�ɕ\����ƌ����܂��B
a+bi�̓�������-a-bi, b-ai, -b+ai������Aa-bi�̓�������-a+bi, -b-ai, b+ai������܂��B
�Ȃ̂ŁA�����P��i�̌W������ƂȂ铯�����̓K�E�X�������̘a�ɂ͕\���܂���B
(3)�L���f��p��p �� 3 (mod 4)�̏ꍇ�Ap���g���K�E�X�f���ł���B
p�͊�Ȃ̂ŁA����L������w�����݂���p = 2w+1 = (w+1)^2+(wi)^2��2�̃K�E�X�������̘a�ɕ\���܂��B
p�̓�������-p, pi, -pi������܂����A�����P��i�̌W������ƂȂ铯�����̓K�E�X�������̘a�ɂ͕\���܂���B
�ȏォ��A1+i�ȊO�̃K�E�X�f���͂��̓������̒���2�̃K�E�X�������̘a�ɕ\������̂����݂���̂ŁA
Im(x)�������ł���K�E�X����x���K�E�X�f��1+i(���������܂�)��������Ɉ����Ɏ��ĂA
x�̓������̒���2�ȉ��̃K�E�X�������̘a�ɕ\������̂����݂���ƌ�����Ǝv���܂��B
�����āA�K�E�X�f��1+i(���������܂�)�����Ɉ����Ɏ��ĂA
x��3�ȉ��̃K�E�X�������̘a�ɕ\����ƌ�����Ǝv���܂��B
# �����ԈႢ�E���Ⴂ���Ă���\��������܂��̂ŁA��L���_�͉L�ۂ݂ɂ���
# ����҂���̕��ŗǂ������肢�܂��B
|
|
|
| ��52402 / ResNo.8) |
�@Re[1]: �K�E�X�����̕����a
|
�����e��/ ����҂�5�� ��ʐl(7��)-(2023/12/05(Tue) 20:33:14)
 | WIZ�l�ԐM���肪�Ƃ��������܂��B
�K�E�X�f���̕������a�ɂ��ďڂ������́E������Ē������ӂ��܂��B
�Љ�Ē������P������(2u-1)+2vi��(2u-1)-2vi���K�E�X�f���ł���K�v���Ȃ��̂Ŕėp���������ł��ˁB
�c��̓K�E�X����y��Re(y)��Im(y)�����ɋ����̏ꍇ�ł��B
y=2u+2vi={(1+i)^2}{v-ui}�����猋��u�������ł��邱�Ƃ��K�v��
u=-2w�Ƃ����v+2wi�ɂ��ĕ��͂���Ƃ����ŏ��̖��ɖ߂��Ă��܂��܂��ˁB
��������K�E�X�f���̍\���Ȃǂ܂��܂������g�����s�ǂł͂���܂���
�{�X���͂���ɂďI���Ƃ����Ē����܂��B
|
|
|
���L�����X�g /
���X�L���\�� ��
[�e�L��-8]
|