lim x→0 sinx x =1 の関係を導く。

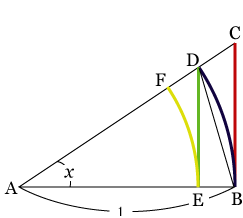
右のような図形を考える。AB＝１，∠BAC＝ｘ （弧度法），弧BDは半径１，弧EFは半径 cosx である。このとき，

sinx ＝DE， x ＝弧BD 　

よって，図形を用いて説明すると，

sinx x = DE 弧BD

となる。直感的に，この値は１より小さい値であるとわかる。

予備知識として，弧EF（ xcosx ），DE（ sinx ），弧BD（ x ），BC（ tanx ）の長さの関係を導いておくことにする。

扇形AEFの面積＝ 1 2 x ( cosx ) 2 ，三角形AED＝ 1 2 cosxsinx ，三角形ABD＝ 1 2 sinx

扇形ABDの面積＝ 1 2 x ，三角形ABC＝ 1 2 tanx

扇形AEFの面積＜三角形AED より，

1 2 x ( cosx ) 2 < 1 2 cosxsinx⇒xcosx<sinx

三角形ABD＜扇形ABDの面積＜三角形ABC より

1 2 sinx< 1 2 x< 1 2 tanx⇒sinx<x<tanx

弧EF（ xcosx ）＜DE（ sinx ）＜弧BD（ x ）＜BC（ tanx ）  ・・・・・・(1)

となる。

sinx x を求めるとき，はさみうちの手法を用いることにする。(1)の関係より，

xcosx x < sinx x < x x ⇒cosx< sinx x <1

となり， x→0  ならば， cosx→1  となり

lim x→0 sinx x =1

が導かれる。また，

sinx tanx < sinx x < sinx sinx ⇒cosx< sinx x <1

となり同様に，

lim x→0 sinx x =1

が導かれる。

【関連ページ】
数学II，数学IIIC，極限の基本式