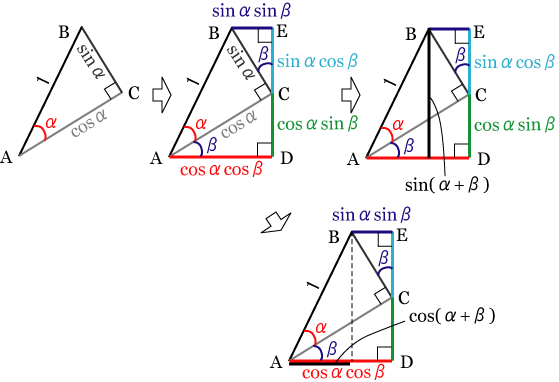
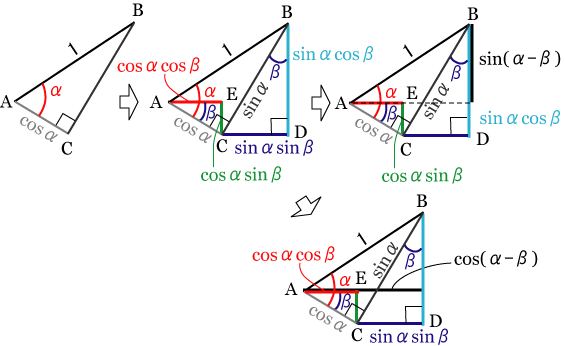
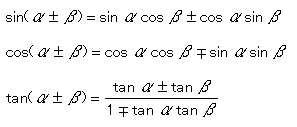|
その2
この導出はスマートでない。
α+β<90°
の場合について図形を用いて導出する。
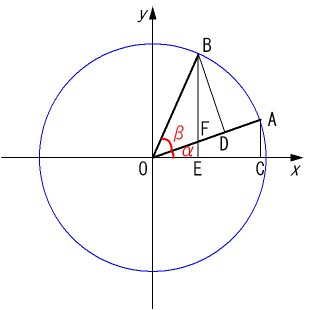
原点を中心として半径1の円周上に、x軸から角度α移動した点をAさらに角度β移動した点をBとする。点Aよりx軸に垂線を降ろしx軸との交点をC、点BからOAに垂線を降ろしOAとの交点をD、点Bよりx軸に垂線を下ろしx軸との交点をEとする。
△FOE∽△FBD(∠OFE=∠BFD、∠OEF=∠BDE=90°)より
EF OE
= DF
BD ・・・・・・(1)
OE=cos(
α+β
) ・・・・・・(2)
EF=sinα
cos( α+β
) cosα
( ∵△OCA∽△OEF
) ・・・・・・(3)
BD=sinβ
・・・・・・(4)
DF=OD−OF
=cosβ−
cos( α+β
) cosα
・・・・・・(5)
(1)に(2)、(3)、(4)、(5)を代入すると
sinα
cos( α+β
) cosα
cos(
α+β
) =
cosβ−
cos( α+β
) cosα
sinβ
sinα
cosα =
cosβ−
cos( α+β
) cosα
sinβ
sinαsinβ=cosαcosβ−cos(
α+β
)
よって
cos(
α+β
)=cosαcosβ−sinαsinβ
・・・・・・(6)
β
に −β
をあてはめるて、
cos( −β
)=cosβ
、 sin(
−β )=−sinβ
を用いると
cos(
α−β
)=cosαcosβ+sinαsinβ
・・・・・・(7)
BE=BF+EF
・・・・・・(8)
BE=sin(
α+β
) ・・・・・・(9)
BF=
BD cosα
( ∵∠EOD=∠EBD
)
=
sinβ cosα
( ∵BD=sinβ
) ・・・・・・(10)
(6)に(9)、(10)、(3)を代入すると
sin( α+β
)=sinα
cos( α+β
) cosα
+ sinβ
cosα
sin(
α+β
)=sinα
cosαcosβ−sinαsinβ
cosα
+ sinβ
cosα
sin(
α+β )=sinαcosβ+
− sin
2 αsinβ+sinβ
cosα
sin(
α+β
)=sinαcosβ+
( 1−
sin 2 α
)sinβ
cosα
sin(
α+β )=sinαcosβ+
( cos
2 α )sinβ
cosα
よって
sin(
α+β
)=sinαcosβ+cosαsinβ
・・・・・・(11)
β
に −β
をあてはめるて、
cos( −β
)=cosβ
、 sin(
−β )=−sinβ
を用いると
sin(
α−β
)=sinαcosβ−cosαsinβ
・・・・・・(12)
|