( a+b ) n = n C 0 a n + n C 1 a n−1 b+ n C 2 a n−2 b 2 +⋯⋯+ n C r a n−r b r +⋯⋯+ n C n b n = ∑ r=0 n n C r a n−r b r

一般項： n C r a n−r b r      ( r=0,1,2,⋯⋯,n )

二項係数： n C r = n! r!( n−r ) ! = n( n−1 )( n−2 )⋯( n−r+1 ) r! n C r = n−1 C r−1 + n−1 C r      ( n≥2 ),      n C r = n C n−r      特に      n C 0 = n C n =1

二項定理の導出
( a+b ) n の二項展開を n=1 から順に計算してみる。

( a+b ) 1 =1·a+1·b

( a+b ) 2 =( a+b )( a+b ) =( a+b )a+( a+b )b =aa+ba+ab+bb    ( 単項式の数は2×2=4 ) =1· a 2 +1·ab+1·ab+1· b 2 =1· a 2 +( 1+1 )ab+1· b 2 =1· a 2 +2·ab+1· b 2

( a+b ) 3 = ( a+b ) 2 ( a+b ) ={ ( a+b )a+( a+b )b }( a+b ) ={ ( a+b )a+( a+b )b }a+{ ( a+b )a+( a+b )b }b =aaa+baa+aba+bba+aab+bab+abb+bbb    ( 単項式の数は2×2×2=8 ) ={ 1· a 2 +2·ab+1· b 2 }a+{ 1· a 2 +2·ab+1· b 2 }b =1· a 3 +2· a 2 b+1·a b 2 +1· a 2 b+2·a b 2 +1· b 3 =1· a 3 +( 2+1 ) a 2 b+( 1+2 )a b 2 +1· b 3 =1· a 3 +3· a 2 b+3·a b 2 +1· b 3

( a+b ) 4 = ( a+b ) 3 ( a+b ) =[ { ( a+b )a+( a+b )b }a+{ ( a+b )a+( a+b )b }b ]( a+b ) =[ { ( a+b )a+( a+b )b }a+{ ( a+b )a+( a+b )b }b ]a+[ { ( a+b )a+( a+b )b }a+{ ( a+b )a+( a+b )b }b ]b =aaaa+baaa+abaa+bbaa+aaba+baba+abba+bbba+aaab+baab+abab+bbab+aabb+babb+abbb+bbbb     ( 単項式の数は2×2×2×2=16 ) =( 1· a 3 +3· a 2 b+3·a b 2 +1· b 3 )a+( 1· a 3 +3· a 2 b+3·a b 2 +1· b 3 )b =1· a 4 +3· a 3 b+3· a 2 b 2 +1·a b 3 +1· a 3 b+3· a 2 b 2 +3·a b 3 +1· b 4 =1· a 4 +( 3+1 ) a 3 b+( 3+3 ) a 2 b 2 +( 1+3 )·a b 3 +1· b 4 =1· a 4 +4· a 3 b+6· a 2 b 2 +4·a b 3 +1· b 4

以上4乗まで計算した。これらから， ( a+b ) n を展開すると単項式は 2 n でき， a n−r b r の単項式は a と b から成る n 個の文字列中から b の文字が入る位置を r 個選ぶ組合せに等しいことが推測できる。 よって，

( a+b ) n = ∑ r=0 n n C r a n−r b r           ・・・・・・(1)

となることがわかる。これを数学的帰納法を用いて証明する。

n=1 のとき，

( a+b ) 1 = 1 C 0 a 1 b 0 + 1 C 1 a 0 b 1 =a+b

となり，(1)は成り立つ。

n=k のとき，(1)が成りたつと仮定すると，

( a+b ) k = ∑ r=0 k k C r a k−r b r

すると，

( a+b ) k+1	=( a+b ) ( a+b ) k
	=( a+b ) ∑ r=0 k k C r a k−r b r
	= ∑ r=0 k k C r a· a k−r b r + ∑ r=0 k k C r a k−r b· b r
	= ∑ r=0 k k C r a k−r+1 b r + ∑ r=0 k k C r a k−r b r+1
	第2項の ∑ r=0 k k C r a k−r b r+1 において r+1=s  （ r=s−1  ）とおくと，
	= ∑ r=0 k k C r a k−r+1 b r + ∑ s=1 k+1 k C s-1 a k−r+1 b s
	第2項の s  を r に書き換えて，式を少し変形すると，
	= ∑ r=0 k k C r a ( k+1 )−r b r + ∑ r=1 k+1 k C r-1 a ( k+1 )−r b r
	= k C 0 a k+1 + ∑ r=1 k k C r a ( k+1 )+r b r + ∑ r=1 k k C r−1 a ( k+1 )+1 b r + k+1 C k+1 b k+1
	= k C 0 a k+1 + ∑ r=1 k k C r a ( k+1 )+1 b r + ∑ r=1 k k C r−1 a ( k+1 )+1 b r + k+1 C k+1 b k+1
	= k C 0 a k+1 + ∑ r=1 k ( k C r + k C r−1 ) a ( k+1 )+1 b r + k+1 C k+1 b k+1
	k C r + k C r−1 = k( k−1 )( k−2 )⋯( k−r+1 ) r! + k( k−1 )( k−2 )⋯( k−r+2 ) ( r−1 )! = k( k−1 )( k−2 )⋯( k−r+2 ) ( r−1 )! ( k−r+1 r +1 ) = ( k+1 )k( k−1 )( k−2 )⋯( k−r+2 ) r! = k+1 C r より （この関係からパスカルの三角形が得られる）
	= k C 0 a k+1 + ∑ r=1 k k+1 C r a ( k+1 )+1 b r + k+1 C k+1 b k+1
	= ∑ r=0 k+1 k+1 C r a ( k+1 )+1 b r

よって， n=k+1 のときも(1)が成り立ち，数学的帰納法により，(1)はすべての自然数 a  に対して成り立つ。

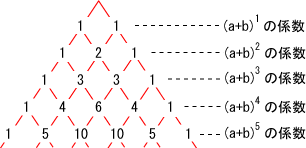
( a+b ) n の係数は，上述した具体的な計算事例と k C r + k C r−1 = k+1 C r の関係から，パスカルの三角形が得られる。

パスカルの三角形を下に示す。

【関連ページ】
数学A