定理:
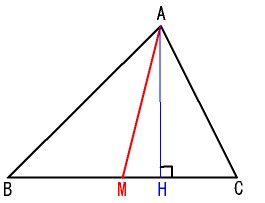
△ABCの辺BCの中点をMとすると
である。
証明:
三平方の定理より,
一方
【関連ページ】
数学A
| 中線定理 by 数学ナビゲーター | 最終更新日 2004年3月31日 | |||||||
| 数式を正常に表示するにはMathPlayerのインストールが必要です。詳しくはホームページを見てください。 |
||||||||
|
定理: △ABCの辺BCの中点をMとすると である。 証明: 三平方の定理より, 【関連ページ】 |
 |
|||||||
|
|
||||||||
|
|
||||||||
| © 2002 Crossroad. All rights reserved. |