|
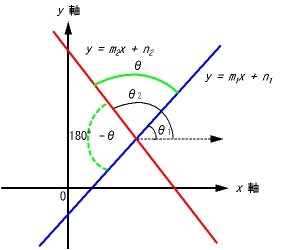
2つの直線の方程式を とすると,上記2直線のなす角 導出計算: 右図参照。tanの定義より 2直線のなす角は よって,(1),(2)より, 2直線のなす角 となる。 【関連ページ】 |
 |
|||||
|
|
||||||
| 2直線のなす角 by 数学ナビゲーター | 最終更新日 2004年3月31日 | |||||||||||||||||||
| 数式を正常に表示するにはMathPlayerのインストールが必要です。詳しくはホームページを見てください。 |
||||||||||||||||||||
|
||||||||||||||||||||
| © 2002 Crossroad. All rights reserved. |