xy平面において,x軸に実数,y軸に虚数を対応させて、複素数を表したものを複素平面という。
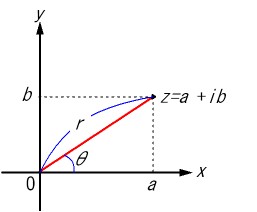
複素数
複素数z の絶対値の定義:
すなわち、複素平面状の原点Oからz までの距離r となる。
また,x 軸と原点Oと点z の結ぶ直線Oz のなす角をθ とする。このθ をzの偏角といい,arg z で表す。z をr とθ を用いても表すことができる。
この表現方法をz の極形式という。
| 複素平面 by 数学ナビゲーター | 最終更新日 2004年3月31日 | |||||||
| 数式を正常に表示するにはMathPlayerのインストールが必要です。詳しくはホームページを見てください。 |
||||||||
|
xy平面において,x軸に実数,y軸に虚数を対応させて、複素数を表したものを複素平面という。 |
||||||||
 |
||||||||
|
複素数 複素数z の絶対値の定義: すなわち、複素平面状の原点Oからz までの距離r となる。 また,x 軸と原点Oと点z の結ぶ直線Oz のなす角をθ とする。このθ をzの偏角といい,arg z で表す。z をr とθ を用いても表すことができる。 この表現方法をz の極形式という。 |
||||||||
|
|
||||||||
| © 2002 Crossroad. All rights reserved. |