| ||||
542×640 => 211×250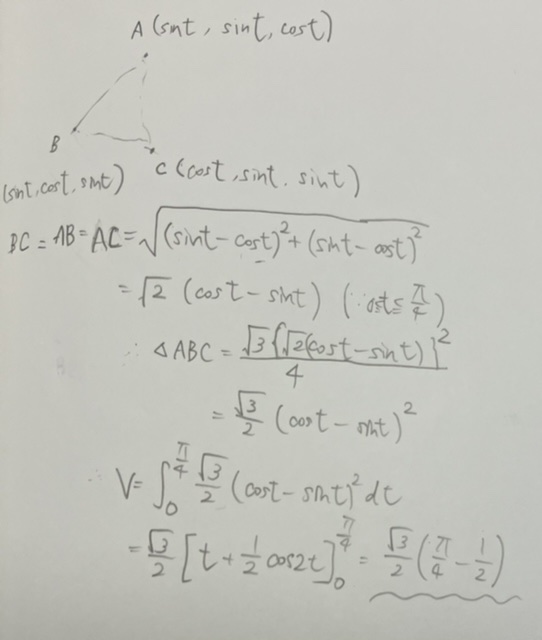 569CB113-ABD8-4A92-9782-9D776D1652A4.jpeg/50KB | ||||
http://www.youtube.com/channel/UCHRwEUVvKzCUqRDRYpKam6A
| ||||
http://www.youtube.com/channel/UCHRwEUVvKzCUqRDRYpKam6A
| ||||
http://www.youtube.com/channel/UCHRwEUVvKzCUqRDRYpKam6A
| ||||
| HOME | HELP | 新規作成 | 新着記事 | ツリー表示 | スレッド表示 | トピック表示 | 発言ランク | ファイル一覧 | 検索 | 過去ログ |
| ||||
542×640 => 211×250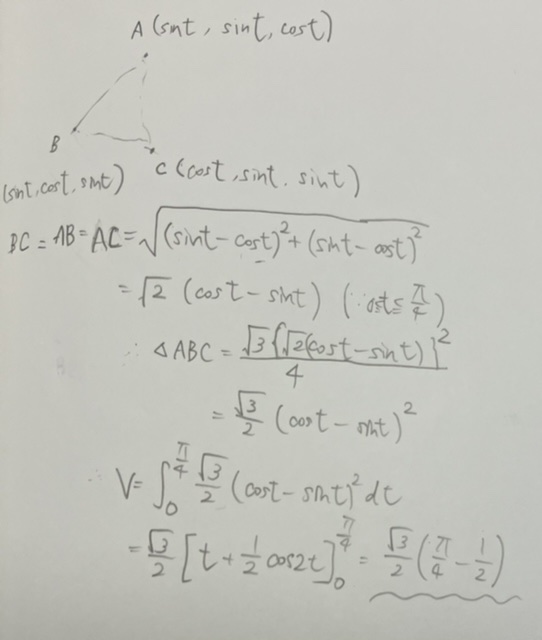 569CB113-ABD8-4A92-9782-9D776D1652A4.jpeg/50KB | ||||
http://www.youtube.com/channel/UCHRwEUVvKzCUqRDRYpKam6A
| ||||
http://www.youtube.com/channel/UCHRwEUVvKzCUqRDRYpKam6A
| ||||
http://www.youtube.com/channel/UCHRwEUVvKzCUqRDRYpKam6A
| ||||
| このトピックに書きこむ |
|---|
| HOME | HELP | 新規作成 | 新着記事 | ツリー表示 | スレッド表示 | トピック表示 | 発言ランク | ファイル一覧 | 検索 | 過去ログ |