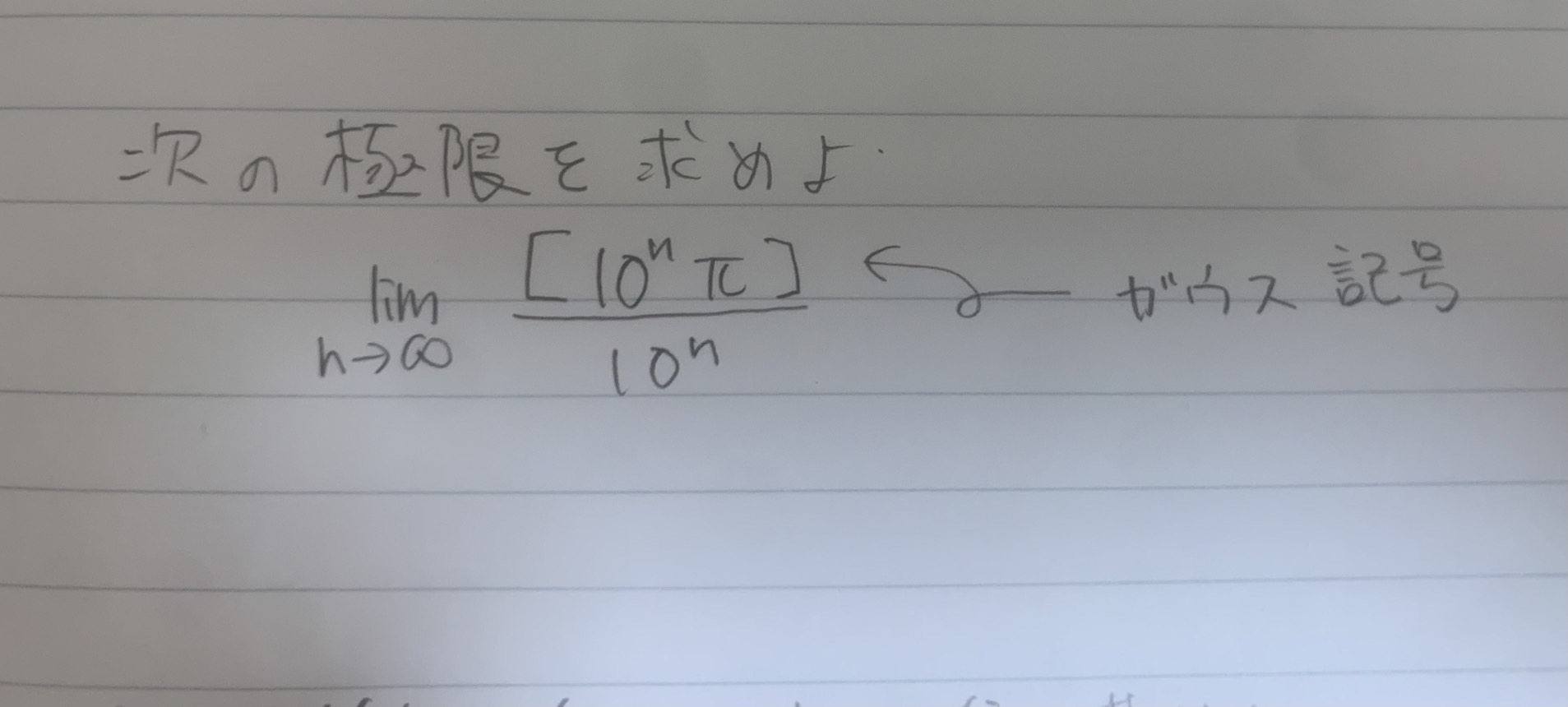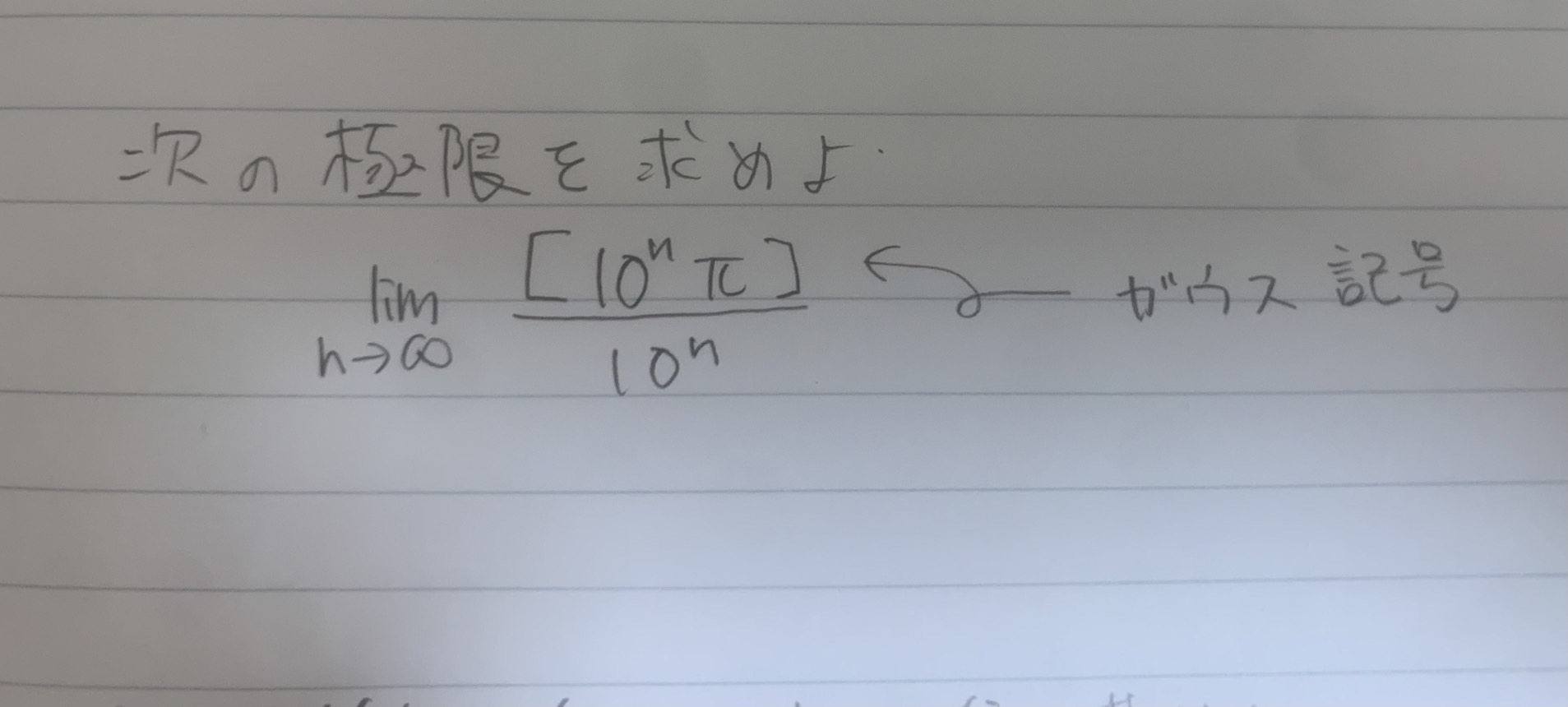 | 2023/12/30(Sat) 22:36:53 編集(投稿者)
πを以下の様な無限級数と考えます。
π = 3.1415・・・
= 3+1/10+4/(10^2)+1/(10^3)+5/(10^4)+・・・
ここでπを10進小数で表した時の各桁の数字を数列と見なし、
a[0] = 3, a[1] = 1, a[2] = 4, a[3] = 1, a[4] = 5, ・・・
とすれば、
π = Σ[k=0,∞]{a[k]/(10^k)} = Σ[k=0,∞]{a[k](10^(-k))}
と表せます。
lim[n→∞]{[(10^n)π]/(10^n)}
= lim[n→∞]{[(10^n)Σ[k=0,∞]{a[k](10^(-k))}]/(10^n)}
= lim[n→∞]{[Σ[k=0,∞]{a[k](10^(n-k))}]/(10^n)}
ガウスの記号の中の小数部分、つまり正で1未満となる部分は無視できますから、
# 厳密には、lim[n→∞]{[Σ[k=0,∞]{a[k](10^(n-k))}]/(10^n)}において、
# k > nの部分の和は、
# Σ[k=n+1,∞]{a[k](10^(n-k))} < Σ[k=1,∞]{9*(10^(-k))} = 9*(1/10)/(1-(1/10)) = 1
# なので、ガウスの記号内のΣ[k=n+1,∞]{a[k](10^(n-k))}の値は無視できるということです。
lim[n→∞]{[Σ[k=0,∞]{a[k](10^(n-k))}]/(10^n)}
= lim[n→∞]{(Σ[k=0,n]{a[k](10^(n-k))})/(10^n)}
= lim[n→∞]{Σ[k=0,n]{a[k](10^(-k))}}
= π
となります。
|
このトピックをツリーで一括表示