| ||||
| ||||
| ||||
| ||||
546×347 => 250×158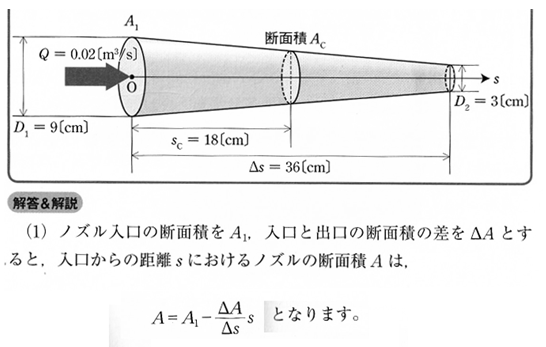 1710565407.png/186KB | ||||
| ||||
500×340 => 250×170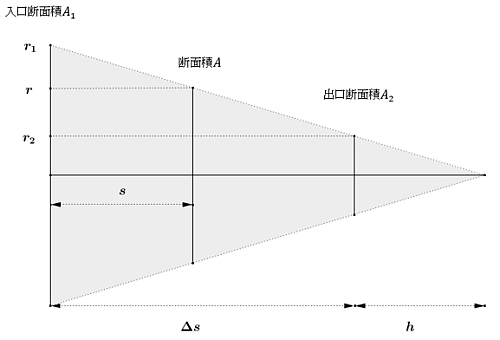 1710565700.png/167KB | ||||
| ||||
380×322 => 250×211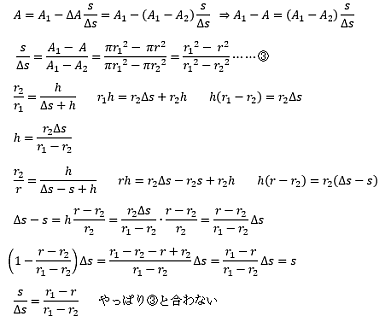 1710566260.png/120KB | ||||
| ||||
| ||||
| ||||
| ||||
| HOME | HELP | 新規作成 | 新着記事 | ツリー表示 | スレッド表示 | トピック表示 | 発言ランク | ファイル一覧 | 検索 | 過去ログ |
| ||||
| ||||
| ||||
| ||||
546×347 => 250×158 1710565407.png/186KB | ||||
| ||||
500×340 => 250×170 1710565700.png/167KB | ||||
| ||||
380×322 => 250×211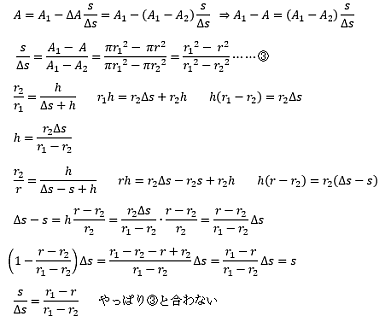 1710566260.png/120KB | ||||
| ||||
| ||||
| ||||
| ||||
| このトピックに書きこむ |
|---|
| HOME | HELP | 新規作成 | 新着記事 | ツリー表示 | スレッド表示 | トピック表示 | 発言ランク | ファイル一覧 | 検索 | 過去ログ |