|
|
|
点P
( x 0
, y 0
, z 0
) を通り,法線ベクトルが
n →
=( a,b,c
) の平面の方程式は
a(
x− x
0 )+b(
y− y
0 )+c(
z− z
0 )=0
と表わされる。また,平面の方程式は一般に
ax+by+cz+d=0
(一般形)
と表される。このとき,平面の法線ベクトルは
n →
=( a,b,c
) となる。
【用語の説明】
法線ベクトル:平面に垂直なベクトルのこと。
|
|
|
|
|
【平面の方程式の導出】
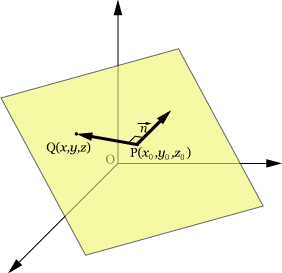
平面は,空間中の点と平面に垂直な法線ベクトルが決まれば,一意的に決まる。平面上の点Pの座標を
( x 0
, y 0
, z 0
) ,法線ベクトルを
n →
=( a,b,c
) とし,平面上の任意の点Qの座標を
( x,y,z
) とすると,ベクトル
PQ ⟶
は平面に含まれる。
n →
は平面の法線ベクトルなので,
n →
と
PQ ⟶
のなす角は90°である。よって,
n →
· PQ
⟶ =0
ここを参照
となる。この関係から,
(
a,b,c
)·(
x− x 0
,y− y
0 ,z−
z 0 )=0
a(
x− x 0
)+b(
y− y 0
)+c(
z− z 0
)=0
となり,平面の方程式が求まる。
|
 |
|
|
【平面の方程式の求め方のいろいろ】
■空間中の3点で決まる平面の方程式
空間中の3点をA
( a x
, a y
, a z
) ,B
( b x
, b y
, b z
) ,C
( c x
, c y
, c z
) とする。3点を含む平面上の点をP
( x,y,z
) とすると,
AB ⟶
と
AC ⟶
をもちいて
AP ⟶
を表すと
m AB
⟶ +n
AC ⟶
= AP
⟶
m ,
n は媒介変数。これを座標成分で表すと,
m{
( b x
, b y
, b z
)−(
a x ,
a y , a
z ) }+n{
( c x
, c y
, c z
)−(
a x ,
a y , a
z ) }={
( x,y,z
)−(
a x ,
a y , a
z ) }
( m(
b x −
a x )+n(
c x −
a x ),m(
b y −
a y )+n(
c y −
a y ),m(
b z −
a z )+n(
c z −
a z )
)=(
x− a x
,y− a
y ,z−
a z )
{
m(
b x − a
x )+n(
c x −
a x )=x−
a x
m( b
y − a y
)+n(
c y −
a y )=y−
a y
m( b
z − a z
)+n(
c z −
a z )=z−
a z
この関係式から,
m ,
n を消去すると平面の方程式が得られる。
別の方法
平面の方程式の一般形の
ax+by+cz+d=0
に点A,点B,点Cの座標を代入して得られる連立方程式
{ a·
a x +b·
a y +c·
a z +d=0
a·
b x +b·
b y +c·
b z +d=0
a·
c x +b·
c y +c·
c z +d=0
を解いても3点を含む平面の方程式を求めることができる。
【関連ページ】
数学B
|
|
|
|
