2の複素数
とおくと,
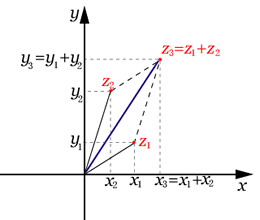
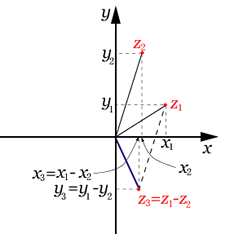
このように複素数の和は実部どうし虚部どうしで和をとる。差は同じように実部どうし虚部どうしで差をとる。これはなんだかベクトルの和と差に似ているね。この複素数の和と差を複素平面を用いて表すと右図のようになる。
| 複素の積 by 数学ナビゲーター | 最終更新日 2004年5月30日 | ||||||
| 数式を正常に表示するにはMathPlayerのインストールが必要です。詳しくはホームページを見てください。 |
|||||||
|
2の複素数 とおくと, このように複素数の和は実部どうし虚部どうしで和をとる。差は同じように実部どうし虚部どうしで差をとる。これはなんだかベクトルの和と差に似ているね。この複素数の和と差を複素平面を用いて表すと右図のようになる。 |
 |
||||||
 |
|||||||
|
|
|||||||
|
|
|||||||
| © 2002 Crossroad. All rights reserved. |