最終更新日
2004年3月31日
【考え方】
2次方程式
(1)を(3)のように書き直すことができれば、2次方程式の解を求めることができる。
(1)を(3)のように書き直すと
【関連ページ】
数学I
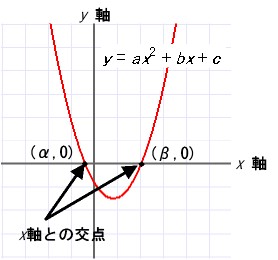
| 2次方程式
|
最終更新日
2004年3月31日
|
|||||||
| 数式を正常に表示するにはMathPlayerのインストールが必要です。詳しくはホームページを見てください。 |
||||||||
|
【考え方】 2次方程式 (1)を(3)のように書き直すことができれば、2次方程式の解を求めることができる。 (1)を(3)のように書き直すと 【関連ページ】 |
||||||||
 |
||||||||
|
|
||||||||
| © 2002 Crossroad. All rights reserved. |