関数のグラフは無数の点の集まりからなっている。よって、グラフの平行移動を理解するには点の移動を理解する必要がある。

【点の移動】

■x 軸方向の移動

点A(x , y )がx 軸方向にp 移動した先の点Bの座標を(x' , y )とする。x とx' の関係は

　　 x'=x+p   ･･･(1)　→　 x=x'−p   ･･･(2)

（x 軸方向のみの移動であるのでy の値は変わらない）

となる。点Aの座標をx' で表すと、(x'-p , y )となる。
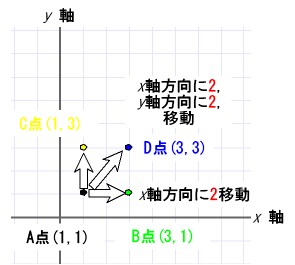
右図にp = 2の場合について具体例を示す。

x 軸方向のグラフの平行移動

■y 軸方向の移動

点A(x , y )がy 軸方向にq 移動した先の点Cの座標を(x , y' )とする。x とx' の関係は

　　 y'=y+q   ･･･(3)　→　 y=y'−q   ･･･(4)

（ｙ 軸方向のみの移動であるのでｘの値は変わらない）

となる。点Aの座標をy' で表すと(x , y'-q )となる。
右の図にq = 2の場合について具体例を示す。

y軸方向のグラフの平行移動

■任意の方向の移動(x軸方向にp 、y 軸方向にq の移動)

点A(x , y )がx 軸方向にp ,y 軸方向にq 移動した先の点Dの座標を(x' , y' )とする。同様にして、点Dの座標をx' とy' で表すと(x'-q , y'-q )となる。
右図にp = 2、q = 2の場合について具体例を示す。

任意の方向のグラフの移動

【関連ページ】
数学I