グラフの平行移動(2)

最終更新日 2004年3月31日

数式を正常に表示するにはMathPlayerのインストールが必要です。詳しくはホームページを見てください。

【グラフの平行移動】

グラフの点を全て同じ方向に移動させると、グラフの平行移動になる。

■ x 軸方向へ p 平行移動する場合
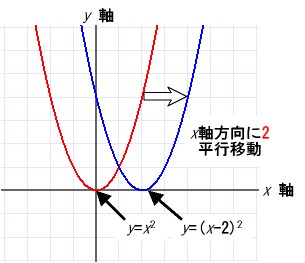
x 軸方向の移動の考え方から y=a x 2 に x=x'−p を代入すると
　　 y=a ( x'−p ) 2
となる。この式の x ′ を x に書き換えると
　　 y=a ( x−p ) 2 2次関数とグラフへ戻る
となり， y=a x 2 を x 軸方向へ p 平行移動した関数が得られる。

右の図にa = 1、p = 2の具体例を示す。

■ y 軸方向へ q 平行移動する場合
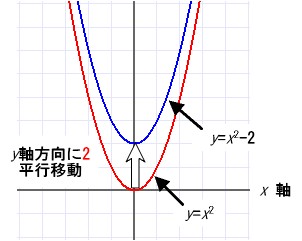
y 軸方向の移動の考え方から y=a x 2 に y=y'−q を代入すると
　　 y'−q=a x 2
となる。この式の y ′ を y に書き換えると
　　 y=a x 2 +q 2次関数とグラフへ戻る
となり， y=a x 2 を y 軸方向へ q 平行移動した関数が得られる。

右の図にa = 1、q = 2の具体例を示す。

■ x 軸方向へ p ， y 軸方向へ q 平行移動する場合
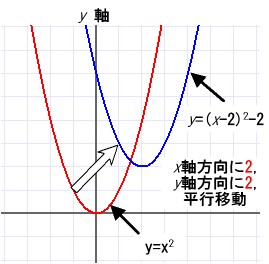
任意の方向の移動の考え方から y=a x 2 に x=x'−p 、 y=y'−q を代入すると
　　 y'−q=a ( x'−p ) 2
となる。この式の x ′ を x に y ′ をy に書き換え p を右辺に移項すると
　　 y'=a ( x'−p ) 2 +q

2次関数とグラフへ戻る
となり， y=a x 2 を x 軸方向へ p，y 軸方向へ q 平行移動した関数が得られる。

右の図にa = 1、p = 2、q = 2の具体例を示す。

【関連ページ】
数学I