余弦定理

　余弦定理　by　数学ナビゲーター

最終更新日2002年6月20日

数式を正常に表示するにはMathPlayerのインストールが必要です。詳しくはホームページを見てください。　

下の表示は左の記述をMathPlayer（フリーソフト）をインストールして数式を正常に表示した状態です。MathPlayerのインストール手順はここを見てください。

三角形の各辺a ,b ,c と各角A ,B ,C の間には余弦
定理という関係がある。

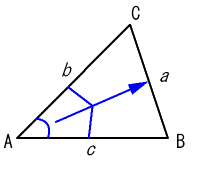
余弦定理： a 2 = b 2 + c 2 −2bccosA b 2 = c 2 + a 2 −2cacosB c 2 = a 2 + b 2 −2abcosC

【証明】

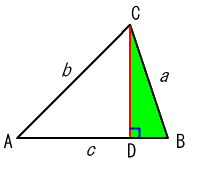
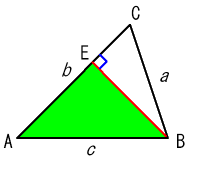
三角形の頂点Cから辺ABに垂線CDを引く。
直角三角形ACDと直角三角形BCDができる。
直角三角形BCDに三平方の定理を用いると、

CB 2 = CD 2 + BD 2 ･･････(1)

CB=a, CD=bsinA, BD=c−bcos A の関係を(1)に代入すると

a 2 = ( bsinA ) 2 + ( c−bcosA ) 2     = b 2 sin 2 A+ c 2 −2cbcosA+ b 2 cos 2 A     = b 2 ( sin 2 A+ cos 2 A )+ c 2 −2cbcosA     = b 2 + c 2 −2bccosA ∴ a 2 = b 2 + c 2 −2bccosA

A =90°, 鈍角の場合の証明は省略

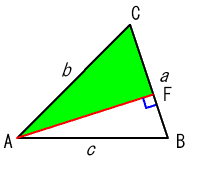
同様にして、

b 2 = c 2 + a 2 −2cacosB c 2 = a 2 + b 2 −2abcosC

も求められる

【問題演習】
センター試験 2002年度本試験数学I・数学A　第2問[2]

【関連ページ】
数学I，正弦定理