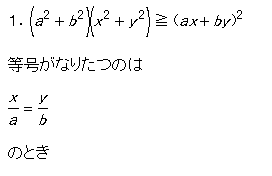|
【証明】
( a 2
+ b 2
)(
x 2 + y
2 )−
( ax+by
) 2
= a 2
x 2 +
a 2 y 2
+ b 2
x 2 +
b 2 y 2
− a 2
x 2 −2abxy−
b 2 y 2
= a
2 y 2
−2abxy+
b 2 x 2
= (
ay−bx
) 2 ≧0
∴
( a 2
+ b 2
)(
x 2 + y
2 )≧
( ax+by
) 2
因数分解、平方完成で不等式を証明している。不等式の証明ページを参照。
等号が成り立つのは
ay−bx=0→ay=bx
の場合である。
a≠0,b≠0
であれば,
x a =
y b の場合である。
2. (
a 2
+ b 2 +
c 2 )(
x 2 +
y 2 + z
2 )≥
( ax+by+cz
) 2
等号がなりたつのは
x a =
y b = z
c
のとき
【証明】
(
a 2 +
b 2 + c
2 )(
x 2 +
y 2 + z
2 )−
( ax+by+cz
) 2
= a 2
x 2 +
a 2 y 2
+ a 2
z 2 +
b 2 x 2
+ b 2
y 2 +
b 2 z 2
+ c 2
x 2 +
c 2 y 2
+ c 2
z 2
−
a 2 x 2
− b 2
y 2 −
c 2 z 2
−2abxy−2bcyx−2cazx
= a
2 y 2
+ a 2
z 2 + b
2 x 2
+ b 2
z 2 + c
2 x 2
+ c 2
y 2 −2abxy−2bcyx−2cazx
=(
a 2 y
2 −2abxy+
b 2 x 2
)+(
b 2 z
2 −2bcyx+
c 2 y 2
)+(
c 2 x
2 −2cazx+
a 2 z 2
)
= ( ay−bx
) 2 +
( bz−cy
) 2 +
( cx−az
) 2 ≧0
∴
( a 2
+ b 2
+ c 2
)( x
2 + y 2
+ z 2
)≧ (
ax+by+cz
) 2
平方完成dで不等式を証明している。不等式の証明ページを参照。
等号が成り立つのは
ay−bx=0,bz−cy=0,cx−az=0→ay=bx,bz=cy,cx=az
の場合である。
a≠0,b≠0,c≠0
であれば,
x a =
y b = z
c の場合である。
3.文字数をn 個に拡張した場合。
(
∑ k=1
n
a k
2 )(
∑ k=1
n
x k 2
)≧
( ∑
k=1 n
a k
x k )
2
4.定積分に拡大した場合
a≦b
ならば,
∫ a b
( f
( x )
2 dx
) ∫ a
b ( g
( x )
2 dx
) ≧ (
∫ a b
( f (
x )g (
x )dx
) ) 2
【関連ページ】
数学A,三角不等式,相加平均と相乗平均の関係
|