2つの複素数
とおくと,
となります。でも,計算はできたがこの商の値がどのような意味をもつのか直感的に理解できないね!
そこで,複素数を極形式で表現して複素数の商の意味を考えてみよう。
とおくと,
三角関数の加法定理と
この結果をよく見ると
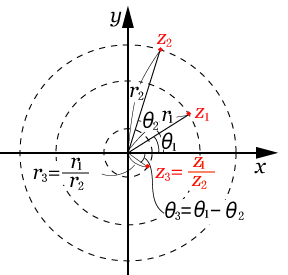
複素数の商は絶対値は商に,偏角は差
になる。 これを図で示すと右の図のようになる。
| 複素数の商 by 数学ナビゲーター | 最終更新日 2004年3月31日 | |||||
| 数式を正常に表示するにはMathPlayerのインストールが必要です。詳しくはホームページを見てください。 |
||||||
|
2つの複素数 とおくと, となります。でも,計算はできたがこの商の値がどのような意味をもつのか直感的に理解できないね! とおくと,
|
||||||
|
この結果をよく見ると 複素数の商は絶対値は商に,偏角は差 になる。 これを図で示すと右の図のようになる。 |
 |
|||||
|
|
||||||
|
|
||||||
| © 2002 Crossroad. All rights reserved. |