2次関数の
　　基本形は　 y=a x 2      ( a≠0 ) 　･･････(1)
　　一般形は　 y=a x 2 +bx+c   ( a≠0 ) 　･･････(2)
で表される。

1. 頂点が原点を通る。
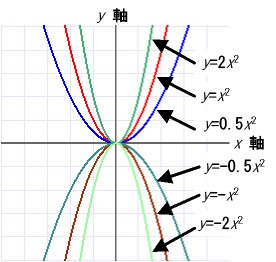
2. a > 0 の場合 、グラフは下に凸になる。
3. a <0の場合、グラフは上に凸になる。

a = -2, -1, -0.5, 0.5, 1, 2の場合を右上のグラフに示す。

一般形は基本形をある方向にある距離だけ並行移動させたものである。一例としてある基本形をx 方向にp ，y 方向にq 平行移動させたグラフを右下のグラフに示している。(点の移動，グラフの平行移動を参照)

ここで、

p=− b 2a 　･･････(3)， q=− b 2 −4ac 4a 　･･････(4)

の関係がある。さらに、詳しく説明する。
y=a x 2 を

x 軸方向にp 平行移動した関数は

一般形を、(8)のように変形することにより2次関数のグラフの特徴を理解することができる。

2次関数のグラフの特徴を表す用語として軸と頂点がある。軸は2次関数グラフの対称軸のことで，この場合のグラフの軸は

x=p   すなわち   x=− b 2a

となる。頂点は2次関数のグラフと軸との交点のことで，この場合のグラフの頂点は

　 ( p,q )　すなわち　( − b 2a ,− b 2 −4ac 4a )

となる。

【関連ページ】
数学I