まず,
すなわち,
理解をさらに深めるために求まった解を極形式に変えてみる(偏角
となり,複素数の絶対値が1で偏角が0°,120°,240°の120°間隔になっている特徴がある。
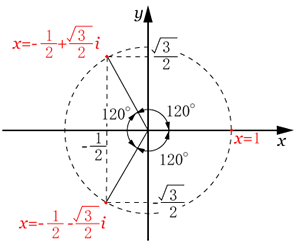
120°(
回転したところに解が存在する。
この特徴をさらに発展させてみる。
| |
最終更新日 2004年3月31日 | |||||||
| 数式を正常に表示するにはMathPlayerのインストールが必要です。詳しくはホームページを見てください。 |
||||||||
|
まず, すなわち, 理解をさらに深めるために求まった解を極形式に変えてみる(偏角 となり,複素数の絶対値が1で偏角が0°,120°,240°の120°間隔になっている特徴がある。 |
||||||||
 |
||||||||
| 半径1の円上に 120°( 回転したところに解が存在する。 |
||||||||
この特徴をさらに発展させてみる。
|
||||||||
|
|
||||||||
|
|
||||||||
| © 2002 Crossroad. All rights reserved. |