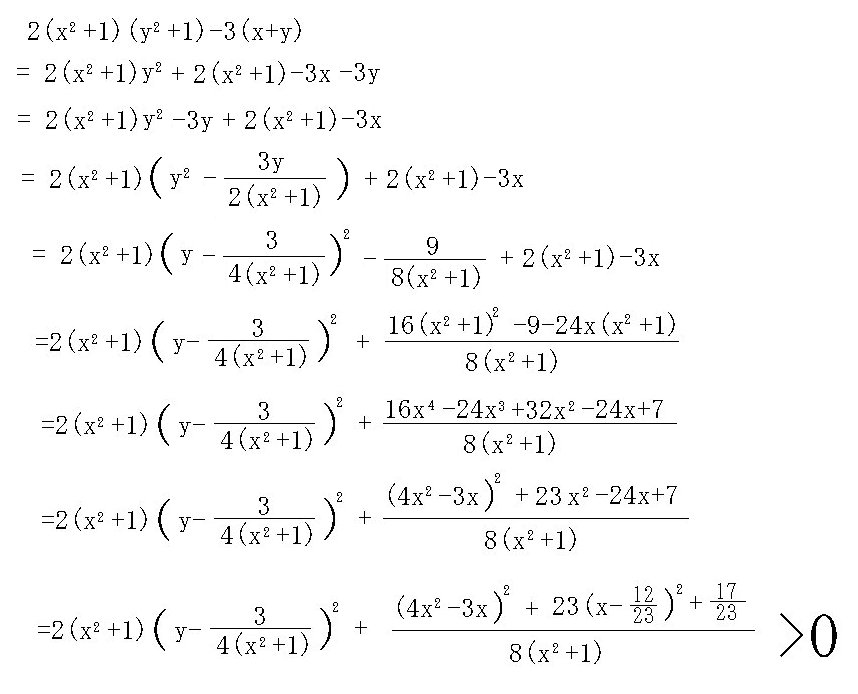���L�����X�g / �����̃X���b�h
/ ����̃X���b�h
�����e��/ ������ ��ʐl(1��)-(2025/02/09(Sun) 06:34:08)
 | �T�C�R����n��ӂ���6�̖ڂ��A����m��ȏ�o��m����
�T�C�R����n+1��ӂ��ē����ڂ��A����m+1��ȏ�o��m����
�ǂ��炪�傫�����m�肽���ł��B
���R�����킹�ċ����Ă��������B
|
|
|
��[�S���X3��(ResNo.1-3 �\��)]
| ��52812 / ResNo.1) |
�@Re[1]: �m��
|
�����e��/ muturajcp ��ʐl(16��)-(2025/04/13(Sun) 09:43:27)
 | 1��m��n
k=0�`n-m�ɑ���
6�ȊO�̖ڂ�k��o��m����(5/6)^k���̌�6�̖ڂ��A����m��o��m����1/6^m
������
�T�C�R����n��ӂ���6�̖ڂ��A����m��ȏ�o��m����
(1/6^m)��[k=0�`n-m](5/6)^k�@�c�@
------------------------------------------
�T�C�R����n+1��ӂ��ē����ڂ��A����m+1��ȏ�o��m����
m=1�̂Ƃ�
1��ڂ�2��ڂ������ڂ��o��m����(1/6)
k=1�`n-1�ɑ���
k��ڂ�k+1��ڂ��قȂ�ڂ��o��m��(5/6)^k
n��ڂ�n+1��ڂ������ڂ��o��m����(1/6)
(1/6)+(1/6)��[k=1�`n-1](5/6)^k
=
(1/6^m)��[k=0�`n-m](5/6)^k
�ƂȂ��ć@�ɓ�����
---
n-m��1�̂Ƃ�
1�`m+1��ڂ������ڂ��o��m����(1/6^m)
n-m=1�̂Ƃ�
1��ڂ�2��ڂ��قȂ�ڂ��o��m��(5/6)
n+1-m�`n+1��ڂ������ڂ��o��m����(1/6^m)
(1/6^m)+(1/6^m)(5/6)
=
(1/6^m)��[k=0�`n-m](5/6)^k
�ƂȂ��ć@�ɓ�����
---
m=2
n=4
�̂Ƃ�
�T�C�R����4+1��ӂ��ē����ڂ��A����2+1��ȏ�o��m����
aaa
(1/6^2)
baaa
(5/6)(1/6^2)
bbaaa
(1/6)(5/6)(1/6^2)
bcaaa
(5/6)(5/6)(1/6^2)
(1/6^2){1+2(5/6)}
>
(1/6^2){1+(5/6)+(5/6)^2}
������
�T�C�R����4��ӂ���6�̖ڂ��A����2��ȏ�o��m�����傫��
|
|
|
| ��52814 / ResNo.2) |
�@Re[2]: �m��
|
�����e��/ �炷���� ��ʐl(14��)-(2025/04/13(Sun) 12:10:23)
 | �Ⴆ��n=5,m=2�̂Ƃ�
3,6,4,6,6
�ł��u6�̖ڂ��A����m��ȏ�o�v�����ƂɂȂ�̂ł́H
|
|
|
| ��52815 / ResNo.3) |
�@Re[3]: �m��
|
�����e��/ muturajcp ��ʐl(17��)-(2025/04/13(Sun) 16:16:37)
 | �ԈႦ�܂����������܂�
m=1�@�̂Ƃ�
1��m��n
k=0�`n-m�ɑ���
6�ȊO�̖ڂ�k��o��m����(5/6)^k���̌�6�̖ڂ��A����m��o��m����1/6^m
������
�T�C�R����n��ӂ���6�̖ڂ��A����m��ȏ�o��m����
(1/6^m)��[k=0�`n-m](5/6)^k�@�c�@
��
m=1�̂Ƃ��������藧���܂���ł���
|
|
|
���L�����X�g /
���X�L���\�� ��
[�e�L��-3]
|