| ■52448 / ResNo.1) |
Re[1]: 解答を教えてください
|
□投稿者/ ポテトフライ 一般人(1回)-(2024/01/13(Sat) 22:11:37)
 | この時期はあなたのような「レポート丸投げ系」の投稿があるから、あまりいい気分はしない。そうでないにしても「何もしてないが答え教えて」というタイプの投稿に思えるので数学の本当に大事な部分を考えることを放棄していて、非常にもったいないことをしていると感じる。
そしてこの内容であれば最低でも学部3年以上の講義であると思われるので、一体何しに大学へ通い、講義を受講しなのか甚だ疑問で仕方ない。(さらに言うと半期もしくは1年でで多様体の基本話一通りとPoincare-Hopfの定理やホモロジー群の話などかなり多岐にわたって話をしているので、控え目に見て相当恵まれた講義であったはずである)
とりあえず各問題に簡単にヒントとなるであろうコメントをしておく。
全ての問題に共通することとして、「問われている概念の定義は何か」ということです。例えば「多様体」について議論しているのに多様体を知らなければ話になりません。
12
多様体の定義を調べましょう。円周S^1が多様体となることは初期の方で理解すべき内容。4つの座標近傍を使う方法や立体射影や正則値定理などで示すことができる。
3
ヤコビ行列や特異点の定義を調べましょう。(多様体論でなくても、多変数の微積分で習う内容だと思う)
4
書いてある通り「はめ込みの定義を述べた上で理由も述べること」
5
部分多様体になることは直ちにわかる(と思う)
「正則」の定義は何ですか?
6
ベクトル場の特異点、そこでの指数の定義。
さらに今与えられたベクトル場の場合にどうなるかを計算します。
また8番でPoincare-Hopfの定理があるので、それとの整合性も確認するとよいでしょう。
7
1-formの積分はどのように計算されますか?講義や演習でやったのではないでしょうか?
8(ここまでの内容を講義で扱うことはほとんどないと思う。非常に素晴らしい)
Poincare-Hopfの定理により特異点は2つであることがわかる。例えば球面上の回転するベクトル場(地球の緯線に沿うベクトル場)は北極点・南極点が特異点である。そのことをもう少し丁寧に説明すればよい(と思う
境界のない2次元多様体の分類を知っているかどうかで大きく難易度が違ってくる。とりあえず球面や射影平面、トーラスなどで考察してみるとよいだろう。
1
とりあえずホモロジー群のランク(Betti数の定義)について計算できなkレばいけない。
2
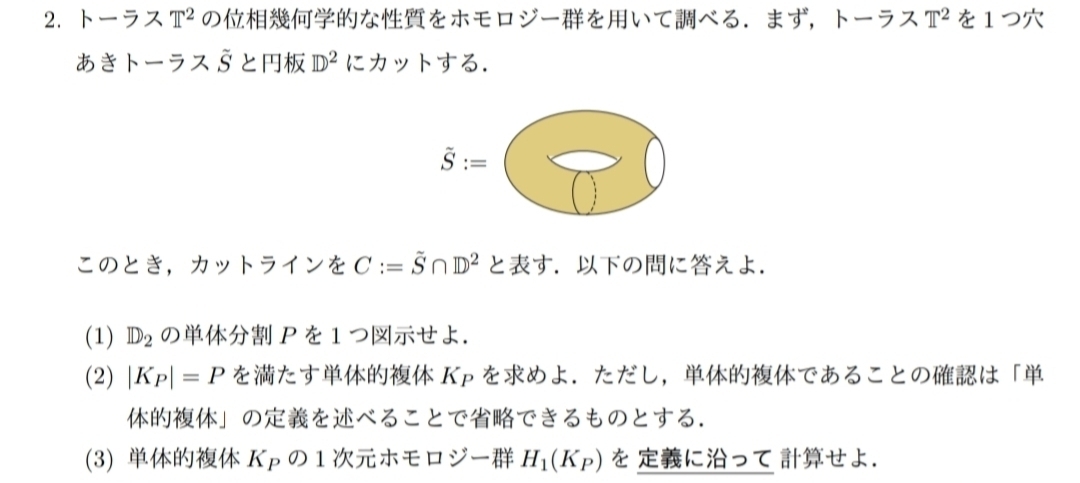
トーラスを切っているが実質的に円盤D^2のホモロジー群を計算することになる。
|
|