■記事リスト / ▼下のスレッド
/ ▲上のスレッド
□投稿者/ 教えて 一般人(1回)-(2023/05/27(Sat) 16:46:08)
 | 0ではない実数a,b,cが
a+ b/c =b+ c/a =c+ a/b
を満たしているとき
|a|=|b|=|c|=1
ですか?
|
|
|
▽[全レス4件(ResNo.1-4 表示)]
| ■52198 / ResNo.1) |
Re[1]: 式の値
|
□投稿者/ X 一般人(5回)-(2023/05/27(Sat) 18:49:57)
 | >>a+ b/c =b+ c/a =c+ a/b
が
(a+b)/c=(b+c)/a=(c+a)/b
の意味であるなら
|a|=|b|=|c|=1
であるとは限りません。
反例)
a=2,b=-1,c=-1のとき
(a+b)/c=(b+c)/a=(c+a)/b
は成立します。
|
|
|
| ■52199 / ResNo.2) |
Re[2]: 式の値
|
□投稿者/ 教えて 一般人(2回)-(2023/05/27(Sat) 19:09:22)
 | 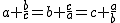 です。 です。
|
|
|
| ■52200 / ResNo.3) |
Re[3]: 式の値
|
□投稿者/ らすかる 一般人(20回)-(2023/05/27(Sat) 19:21:41)
 | a=b=c≠0ならa=b=cがいくつでも成り立ちますので、|a|=|b|=|c|=1とは限りません。
|
|
|
| ■52201 / ResNo.4) |
Re[4]: 式の値
|
□投稿者/ 教えて 一般人(3回)-(2023/05/27(Sat) 19:30:34)
 | そうでした
新しく書き直します
|
|
|
■記事リスト /
レス記事表示 →
[親記事-4]
|